Lebensdauerberechnung mit unserem internen Tool

Daten für die Lebensdauerberechnung:

  • Geometriedaten der relevanten Bauteile.
  • Belastungssituation als Zeitverlauf (Zum Beispiel Kräfte, Momente, Verschiebungen, Beschleunigungen).
  • Materialdaten und Sicherheiten in Form von z.B. Wöhlerlinien.

Ablauf der Lebensdauerberechnung mit unserem internen Tool:

  • Aufbau und Berechnung eines FE-Modells mit Einheitslastfällen.
  • Ermittlung des multiaxialen Spannungszustandes im Zeitverlauf durch die Skalierung der Einheitslasten aus dem FE-Modell mit den bereitgestellten Zeitverläufen der Belastungsgrößen.
  • Aufbereitung der Zeitserien.
  • Berechnung der Lebensdauer durch Auszählen der Spannungslastwechsel (Hauptspannungsdifferenz oder Ansatz der kritischen Schnittebene) und Nachweisführung mit den Materialdaten und Sicherheiten.

Abbildung 1: Darstellung des Quellcodes

Bereitstellung der Ergebnisse:

  • Die Ergebnisse werden grafisch aufbereitet (beispielsweise durch Plots der Lebensdauer). So können mögliche kritische Stellen der Struktur identifiziert werden.
  • Änderungsvorschläge werden durch langjährige Erfahrung in der Betriebsfestigkeitsberechnung und numerischen Simulation diskutiert, wenn die geforderte Lebensdauer nicht erfüllt wird.
  • Übergeben wird wahlweise eine Kurzpräsentation oder ein prüffähiger Bericht.

Numerisch gestützte Stabilitätsanalyse mittels FEM-Berechnung

Ablauf eines numerisch gestützten Beulsicherheitsnachweises am Beispiel eines Turmes einer Windenergieanalge:

  • Aufbau der Turmsektion als Schalenmodell.
  • Durchführung linearer und nichtlinearer Vorberechnungen.
  • Berücksichtigung unterschiedlicher geeigneter Imperfektionsformen zur Ermittlung der maßgebenden Imperfektionsform (Verwendung von eigenformaffinen und quasi-kollapsaffinen Imperfektionsformen; S. Abbildung 1 und Abbildung 2).
  • Durchführung mehrerer geometrisch und materiell nichtlinearer Berechnungen mit Imperfektionen (GMNIA).
  • Ermittlung der Last-Verschiebungskurven für jede Imperfektionsform zur Bestimmung des minimalen Bemessungswiderstandes (s. Abbildung 3).

Abbildung 1: eigenformaffine Imperfektionsform

Abbildung 2: quasi-kollapsaffine Imperfektionsform

Abbildung 3: Last-Verschiebungskurven für den Stabilitätsnachweis

FEM-Berechnungen von Grout-Verbindungen

Im Offshore-Bereich ist eine Verbindungsart zwischen Pile und Sleeve die Grout-Verbindung. Dabei werden zwei Rohre überlappt und der Zwischenraum wird mit Grout aufgefüllt. Durch die Verwendung von Schubrippen wird ein Durchrutschen verhindert.

Zur Berechnung dieser Verbindung nutzen wir spezielle Materialgesetze wie das Drucker Prager oder Menetrey Willam Materialgesetz. Für die beiden Materialgesetze werden die für Beton typischen Kennwerte einaxiale Druckfestigkeit Rc, einaxiale Zugfestigkeit Rt und biaxiale Druckfestigkeit Rb verwendet. Mit diesen Materialgesetzen werden die Betoneigenschaften gut wiedergegeben. Die Bewertung erfolgt anschließend nach dem Model Code for Concrete Structures 2010.

Im vorliegenden Beispiel wurde eine Grout-Verbindung in kleinem Maßstab simuliert. Es ist deutlich zu sehen, dass sich die Druckstreben im Beton ausbilden und es lokal an den Schubrippen zu einer erhöhten Belastung kommt (s. Abbildung 1).

Abbildung 1: Schematische Darstellung einer Grout-Verbindung (rechts) mit Ergebnissen (links)

Analytische Nachweise für Windenergieanlagen mit unserem internen Tool

Einige Aufgaben benötigen maßgeschneiderte Berechnungen. Für solche Aufgaben entwickeln wir Berechnungstools bei uns im Haus. Damit können wir:

  • analytische Nachweise für Türme von Windenergieanlagen programmunterstützt durchführen.
  • Nachweise effizient und schnell führen.
  • Optimierungspotenzial zielgerichtet benennen.

Dabei werden

  • die Nachweise nach gängigen Normen und Richtlinien geführt (zum Beispiel Eurocode 3, IEC-Richtlinien, DIBt-Richtlinie).
  • kundenspezifische Anforderungen eingepflegt.
  • Aktualisierungen bei den relevanten Normen und Richtlinie eingepflegt.

Die Ausgabe der Ergebnisse erfolgt

  • übersichtlich in Diagrammen.
  • als Detaillösung mit Zwischenergebnissen.

Abbildung 1: Darstellung des Quellcodes (links) und der Ergebnisausgabe der Modalanalyse (rechts)

Nachweis des Antriebsstranges von WindenergieanlageN

Für den Antriebsstrang einer Windenergieanlage müssen verschiedene Bauteile nachgewiesen werden:

  • Nachweis der Lagergehäuse
  • Nachweis des Generatorträgers
  • Nachweis des Maschinenträgers
  • Nachweis der Antriebswelle

Für die Nachweisführung wird aus den CAD-Modellen der relevanten Bauteile ein FE-Modell abgeleitet und die relevanten Bereiche werden fein vernetzt (s. Abbildung 1). Weiterhin wird der Kraftweg von der Rotornabe bis zum Turmkopfflansch abgebildet (s. Abbildung 2). Dabei wird die Lagerung der Antriebswelle berücksichtigt. Es werden z.B. die nachfolgenden Nachweise geführt:

  • Extremlastnachweis
  • Ermüdungsnachweis

Der Ermüdungsnachweis kann mit unserem internen Berechnungstool und den zur Verfügung gestellten Zeitreihen geführt werden.

Abbildung 1: FE-Modell eines Antriebsstranges

Abbildung 2: Verformung eines Antriebsstranges (überhöht dargestellt)

Dynamische FEM-Berechnungen

Ein Beispiel für eine dynamische FEM-Berechnung ist eine Antwort-Spektrum-Analyse. Die Berechnung hat das Ziel, mit relativ geringem Aufwand gute Abschätzungen für die maximalen Beanspruchungen in einer Struktur zu ermitteln. Dabei werden die Ergebnisse aus einer Modalanalyse zusammen mit einem bekannten Anregungsspektrum verwendet, um die Spannungen und Verformungen einer Struktur zu berechnen (s. Abbildung 1). Mit einer Antwort-Spektrum-Analyse können z.B. Motor- und Karosserieanbauteile hinsichtlich der Betriebsfestigkeit bewertet werden.

Abbildung 1: Profil eines Anregungsspektrums

FEM-Berechnungen im Bereich Offshore

Im Bereich der Offshore haben wir umpfangreiche Erfahrungen in den nachfolgenden Bereichen gesammelt:

  • Nachweisführung von Jackets (s. Abbildung 1)
  • Nachweisführung von Monopiles
  • Nachweisführung von Tripiles (s. Abbildung 2)
  • Nachweisführung von Grout-Verbindungen (s. Abbildung 3)
  • Nachweisführung von Suction Buckets
  • Nachweis für mobile Hebebühnen (s. Abbidlung 4)

Für die Berechnung von Offshore-Strukturen werden u.a. Wellenlasten berücksichtigt. Diese werden in einer quasi-statischen FEM-Berechnung aus verschiedenen Richtungen auf das Modell aufgebracht. Für die Definition der Wellenlasten werden äußere Einflüsse wie z.B. Wassertiefe, mariner Bewuchs und das Ausspülen des Meeresbodens an der Verbindung berücksichtigt.

Abbildung 1: FE-Modell eines Jackets

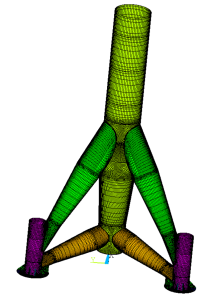Abbildung 2: FE-Modell eines Tripiles

Abbildung 3: FE-Modell einer Grout-Verbindung

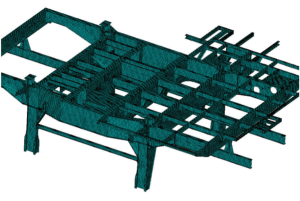Abbildung 4: FE-Modell eine mobilen Hebebühne

FEm-Berechnungen im Bereich Schiffbau

Im Schiffbau haben wir umfangreiche Erfahrungen gesammelt. Dazu gehören FEM-Berechnungen von:

  • Details an Kreuzfahrtschiffen
  • Rumpfsektionen
  • Fensterausschnitten
  • Signalmasten
  • Brücken- und Deckshäusern auf Containerschiffen

FEM-Berechnung im Bereich Schiffbau am Beispiel von Festigkeitsberechnungen für die Kransäulen eines Schwergutschiffe. Zusätzlich zu den Kransäulen sind Ausschnitte in den Querblechen zwischen zwei Decks bezüglich der Festigkeit geprüft worden (s. Abbildung 1).

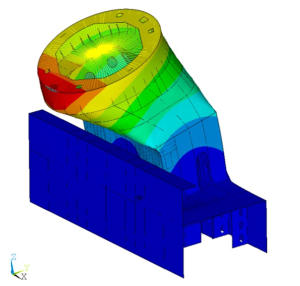Abbildung 1: Verformung der Kransäule (überhlöht dargestellt)

Bewertung von Bauabweichungen und Schadensfällen

Kommt es im laufenden Betrieb zu Schadensfällen (z.B. durch Rotorblatteinschlag oder Anpralllasten) oder bei der Fertigung zu Bauabweichungen, dann kann eine nachträgliche Bewertung der Bauteile dazu führen, dass die betroffenen Bauteile weiter verwendet werden können. Durch unsere umfangreiche Erfahreung in diesem Bereich können wir

  • anhand von einzelnen Messpunkten z.B. im Bauteil vorhandene Beulen nachmodellieren (s. Abbildung 1).
  • anhand von globalen oder lokalen Punktwolken z.B. im Bauteil vorhandene globale oder lokale Beulen modellieren.
  • Bauabweichungen modellieren oder in bestehende Modelle einpflegen.

Im Schadensfall oder bei einer Bauabweichung müssen z.B. die nachfolgenden Nachweise neu geführt werden:

  • Betriebsfestigkeitsnachweis
  • Stabilitätsnachweis
  • Extremlastnachweis

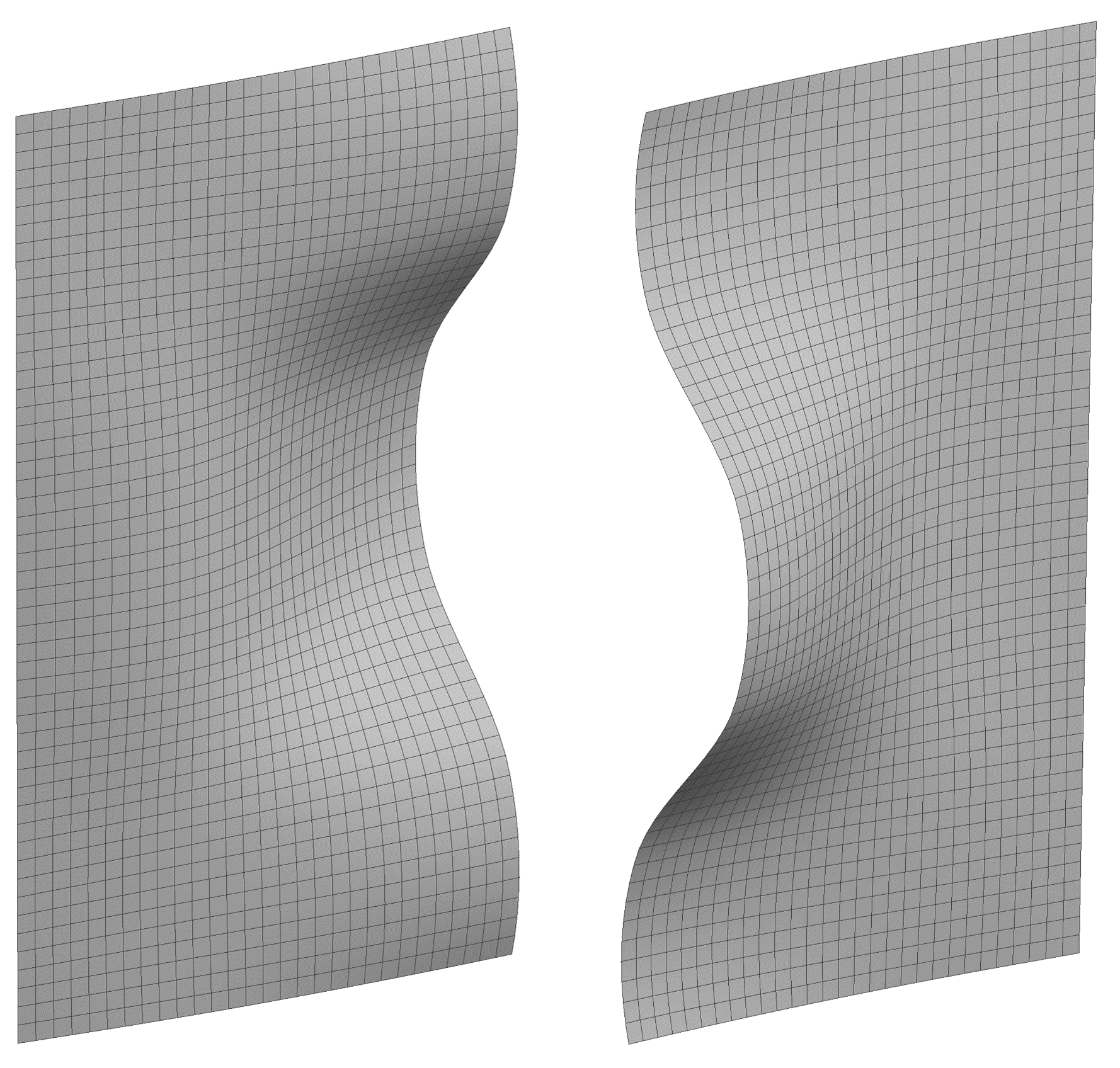Abbildung 1: Anhand von einzelnen Messpunkten modellierte lokale Beule in zwei Ansichten (Schnittdarstellung)